Critical Value Of Correlation Coefficient

Disquisitional Value

Critical value is a cutting-off value that is used to marking the offset of a region where the exam statistic, obtained in hypothesis testing, is unlikely to fall in. In hypothesis testing, the disquisitional value is compared with the obtained test statistic to determine whether the zippo hypothesis has to exist rejected or not.

Graphically, the critical value splits the graph into the acceptance region and the rejection region for hypothesis testing. Information technology helps to check the statistical significance of a exam statistic. In this article, we will learn more about the disquisitional value, its formula, types, and how to calculate its value.

1.	What is Critical Value?
2.	Critical Value Formula
iii.	T Disquisitional Value
four.	Z Critical Value
5.	F Critical Value
6.	Chi-Square Critical Value
vii.	Critical Value Calculation
viii.	FAQs on Disquisitional Value

What is Critical Value?

A critical value tin can be calculated for different types of hypothesis tests. The critical value of a particular examination can be interpreted from the distribution of the test statistic and the significance level. A one-tailed hypothesis examination will have one disquisitional value while a two-tailed test will take two critical values.

Disquisitional Value Definition

Critical value tin can exist defined as a value that is compared to a test statistic in hypothesis testing to determine whether the null hypothesis is to exist rejected or not. If the value of the test statistic is less farthermost than the critical value, then the null hypothesis cannot be rejected. However, if the test statistic is more extreme than the critical value, the zero hypothesis is rejected and the alternative hypothesis is accepted. In other words, the critical value divides the distribution graph into the credence and the rejection region. If the value of the examination statistic falls in the rejection region, then the null hypothesis is rejected otherwise it cannot be rejected.

Disquisitional Value Formula

Depending upon the blazon of distribution the test statistic belongs to, there are different formulas to compute the critical value. The confidence interval or the significance level tin be used to determine a critical value. Given beneath are the dissimilar disquisitional value formulas.

Critical Value Confidence Interval

The critical value for a one-tailed or ii-tailed exam can be computed using the confidence interval. Suppose a confidence interval of 95% has been specified for conducting a hypothesis test. The disquisitional value tin be determined as follows:

Step 1: Subtract the confidence level from 100%. 100% - 95% = 5%.
Step 2: Convert this value to decimals to become \(\alpha\). Thus, \(\alpha\) = 5%.
Stride three: If it is a one-tailed test and then the alpha level will exist the same value in step two. Notwithstanding, if it is a two-tailed test, the alpha level will be divided past 2.
Footstep four: Depending on the type of test conducted the critical value tin be looked upwardly from the corresponding distribution table using the alpha value.

The process used in step four will be elaborated in the upcoming sections.

T Critical Value

A t-test is used when the population standard deviation is not known and the sample size is lesser than 30. A t-test is conducted when the population data follows a Student t distribution. The t disquisitional value can be calculated as follows:

Determine the alpha level.
Subtract ane from the sample size. This gives the degrees of freedom (df).
If the hypothesis test is 1-tailed then use the i-tailed t distribution table. Otherwise, use the two-tailed t distribution table for a 2-tailed exam.
Match the respective df value (left side) and the alpha value (top row) of the tabular array. Find the intersection of this row and column to give the t critical value.

Test Statistic for one sample t test: t = \(\frac{\overline{10}-\mu}{\frac{s}{\sqrt{north}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population hateful, due south is the sample standard deviation and n is the size of the sample.

Test Statistic for ii samples t examination: \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{one}-\mu_{two})}{\sqrt{\frac{s_{1}^{two}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Decision Criteria:

Refuse the null hypothesis if test statistic > t critical value (right-tailed hypothesis exam).
Refuse the nil hypothesis if test statistic < t critical value (left-tailed hypothesis test).
Reject the null hypothesis if the test statistic does not prevarication in the credence region (two-tailed hypothesis test).

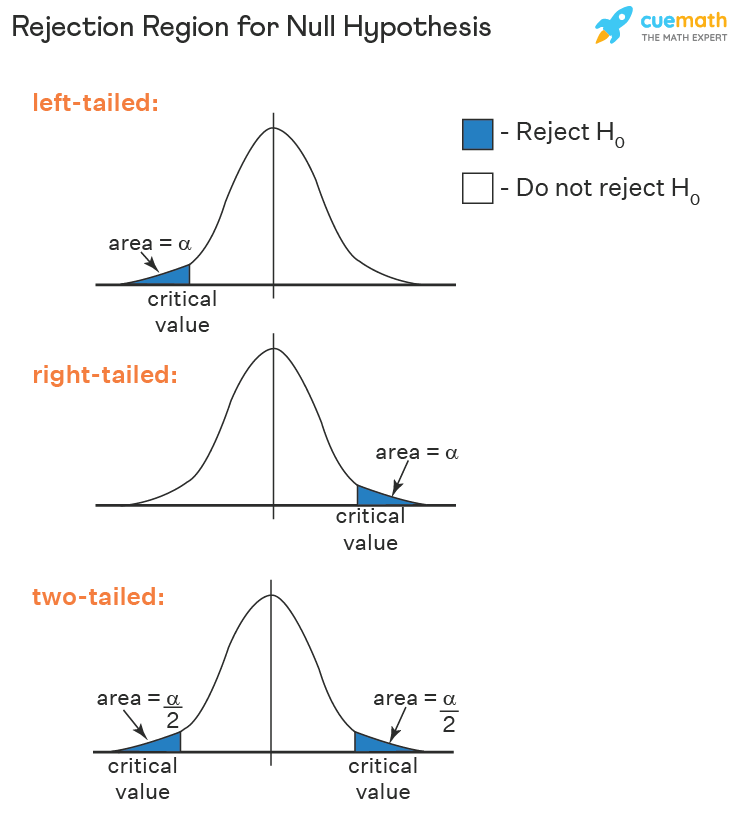
Critical Value

This determination benchmark is used for all tests. Only the test statistic and critical value change.

Z Critical Value

A z test is conducted on a normal distribution when the population standard deviation is known and the sample size is greater than or equal to 30. The z critical value can exist calculated equally follows:

Discover the alpha level.
Subtract the alpha level from ane for a two-tailed exam. For a one-tailed test subtract the alpha level from 0.5.
Wait up the area from the z distribution table to obtain the z critical value. For a left-tailed test, a negative sign needs to be added to the disquisitional value at the end of the adding.

Exam statistic for i sample z test: z = \(\frac{\overline{10}-\mu}{\frac{\sigma}{\sqrt{due north}}}\). \(\sigma\) is the population standard deviation.

Test statistic for ii samples z test: z = \(\frac{(\overline{x_{ane}}-\overline{x_{ii}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{i}^{2}}{n_{one}}+\frac{\sigma_{2}^{ii}}{n_{ii}}}}\).

F Disquisitional Value

The F examination is largely used to compare the variances of two samples. The test statistic so obtained is also used for regression analysis. The f critical value is given as follows:

Find the blastoff level.
Subtract 1 from the size of the get-go sample. This gives the kickoff caste of freedom. Say, x
Similarly, subtract 1 from the second sample size to become the 2nd df. Say, y.
Using the f distribution tabular array, the intersection of the x column and y row will requite the f disquisitional value.

Test Statistic for large samples: f = \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\). \(\sigma_{i}^{2}\) variance of the first sample and \(\sigma_{2}^{2}\) variance of the second sample.

Exam Statistic for small samples: f = \(\frac{s_{ane}^{2}}{s_{2}^{2}}\). \(s_{1}^{1}\) variance of the first sample and \(s_{two}^{2}\) variance of the 2nd sample.

Chi-Square Critical Value

The chi-foursquare test is used to check if the sample information matches the population data. It tin also be used to compare two variables to see if they are related. The chi-square critical value is given as follows:

Identify the alpha level.
Subtract 1 from the sample size to decide the degrees of liberty (df).
Using the chi-foursquare distribution table, the intersection of the row of the df and the column of the alpha value yields the chi-square critical value.

Examination statistic for chi-squared examination statistic: \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\).

Critical Value Adding

Suppose a correct-tailed z test is beingness conducted. The critical value needs to be calculated for a 0.0079 alpha level. Then the steps are as follows:

Decrease the alpha level from 0.5. Thus, 0.5 - 0.0079 = 0.4921
Using the z distribution tabular array find the area closest to 0.4921. The closest surface area is 0.4922. As this value is at the intersection of 2.four and 0.02 thus, the z disquisitional value = 2.42.

Critical Value Calculation

Related Manufactures:

Probability and Statistics
Data Handling
Data

Of import Notes on Disquisitional Value

Disquisitional value can exist divers every bit a value that is useful in checking whether the null hypothesis can be rejected or not past comparing it with the test statistic.
It is the point that divides the distribution graph into the acceptance and the rejection region.
There are four types of critical values - z, f, chi-square, and t.

Examples on Critical Value

Example 1: Find the critical value for a left tailed z test where \(\alpha\) = 0.012.

Solution: First decrease \(\alpha\) from 0.5. Thus, 0.five - 0.012 = 0.488.

Using the z distribution tabular array, z = 2.26.

Withal, as this is a left-tailed z test thus, z = -ii.26

Answer: Disquisitional value = -ii.26
Instance 2: Find the disquisitional value for a two-tailed f test conducted on the following samples at a \(\blastoff\) = 0.025

Variance = 110, Sample size = 41

Variance = 70, Sample size = 21

Solution: \(n_{one}\) = 41, \(n_{2}\) = 21,

\(n_{1}\) - i= xl, \(n_{2}\) - 1 = 20,

Sample i df = twoscore, Sample 2 df = xx

Using the F distribution table for \(\alpha\) = 0.025, the value at the intersection of the 40^th column and 20^thursday row is

F(40, 20) = 2.287

Answer: Critical Value = 2.287
Example 3: Suppose a one-tailed t-test is being conducted on information with a sample size of 8 at \(\blastoff\) = 0.05. Then find the disquisitional value.

Solution: northward = eight

df = 8 - 1 = 7

Using the one tailed t distribution tabular array t(7, 0.05) = ane.895.

Answer: Crititcal Value = 1.895

become to slidego to slidego to slide

Breakup tough concepts through unproblematic visuals.

Math will no longer be a tough subject field, specially when you lot empathise the concepts through visualizations.

Book a Complimentary Trial Grade

FAQs on Critical Value

What is the Critical Value in Statistics?

Critical value in statistics is a cut-off value that is compared with a test statistic in hypothesis testing to bank check whether the nada hypothesis should be rejected or not.

What are the Different Types of Disquisitional Value?

There are iv types of critical values depending upon the type of distributions they are obtained from. These distributions are given every bit follows:

Normal distribution (z critical value).
Student t distribution (t).
Chi-squared distribution (chi-squared).
F distribution (f).

What is the Critical Value Formula for an F test?

To find the critical value for an f examination the steps are as follows:

Find the blastoff level.
Decide the degrees of liberty for both samples past subtracting i from each sample size.
Detect the corresponding value from a one-tailed or two-tailed f distribution at the given alpha level.
This will requite the critical value.

What is the T Critical Value?

The t disquisitional value is obtained when the population follows a t distribution. The steps to find the t critical value are as follows:

Decide the alpha level.
Subtract the sample size number by 1 to become the df.
Use the t distribution table for the blastoff value to become the required critical value.

How to Discover the Critical Value Using a Confidence Interval for a Ii-Tailed Z Test?

The steps to discover the critical value using a confidence interval are as follows:

Decrease the confident interval from 100% and convert the resultant into a decimal value to get the alpha level.
Decrease this value from 1.
Find the z value for the corresponding surface area using the normal distribution tabular array to get the critical value.

Tin can a Critical Value be Negative?

If a left-tailed test is being conducted then the critical value will exist negative. This is considering the critical value volition be to the left of the mean thus, making it negative.

How to Reject Null Hypothesis Based on Critical Value?

The rejection criteria for the cypher hypothesis is given equally follows:

Right-tailed test: Test statistic > critical value.
Left-tailed test: Test statistic < critical value.
Two-tailed test: Reject if the test statistic does non lie in the acceptance region.